Pascal's Triangle

About

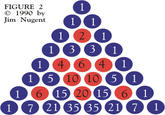
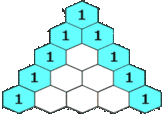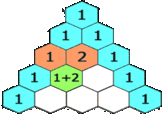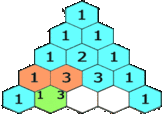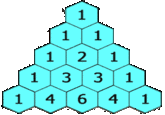
Pascal's Triangleis a triangular formation that is bordered by a series of ones with each interior row being equal to the sum of the two interior rows above. The array illustrates the mathematical concept of binomial coefficients.

Origin

Although Pascal's Triangle is named after French mathematician Blaise Pascal, the triangle was used in China as early as the 11th century, 600 years before the time of Pascal.^[3] The triangle was first developed by mathematician Jia Xian as a tool to find both square and cubic roots.^[2] In the 13th century, it was formally described in the books Xugu Zhaiqi Suanfa and Suanfa Tongbian Benmo by mathematician Yang Hui, giving it the name "Yang Hui's Triangle" in China (shown below).^[2]

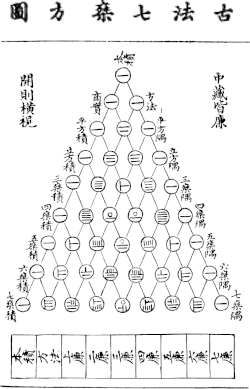
Yang Hui's Triangle

Spread

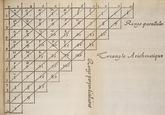
In the 12th century, references to the series of numbers began appearing outside of China in Arabia and Iran.^[3] In 1527, the triangle made its first appearance in Europe in a book on business calculations titled Ein newe und wolgegründete underweisung aller Kauffmanns Rechnung in dreyen Büchern, mit schönen Regeln und fragstücken begriffen by the German mathematician Petrus Apianus. Over a century later in 1665, the triangle was used by Blaise Pascal in Traité du Triangle Arithmétique (shown below), a publication on the calculation of probability. In later publications, mathematicians Pierre Raymond de Montmort and Abraham de Moivre referred to the array as "Pascal's Arithmetic Triangle," cementing the name "Pascal's Triangle" in the western world.

Pascal's Triangle as it appeared in _Traité du Triangle Arithmétique

Notable Examples

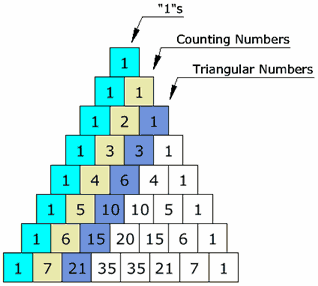
Derivatives

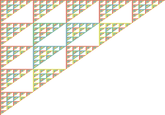
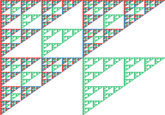
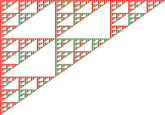
Sierpinkski Triangle

The Sierpinkski triangle is a fractal (shown below) named after Polish mathematician Waclaw Sierpinski, which can be formed from a Pascal's triangle by coloring in only the odd numbers as the number of rows approaches infinity if a fixed perimeter is assumed.

Pascal's Pyramid

Pascal's pyramid^[4] is a tetrahedron that is the three-dimensional analog to Pascal's triangle (shown below).

Bean Machine

The bean machine, or Galton box, is an invention by scientist and mathematician Sir Francis Galton, which consists of a vertical board with rows of pins through which balls are dropped through. The different paths the balls take are determined by the numbers in Pascal's triangle.

History of Reference

External References